Wednesday 27, March 2019 to Friday 29, March 2019




Previous Editions
- March 2015
- March 2016
- March 2017
- March 2018
Learning outcomes
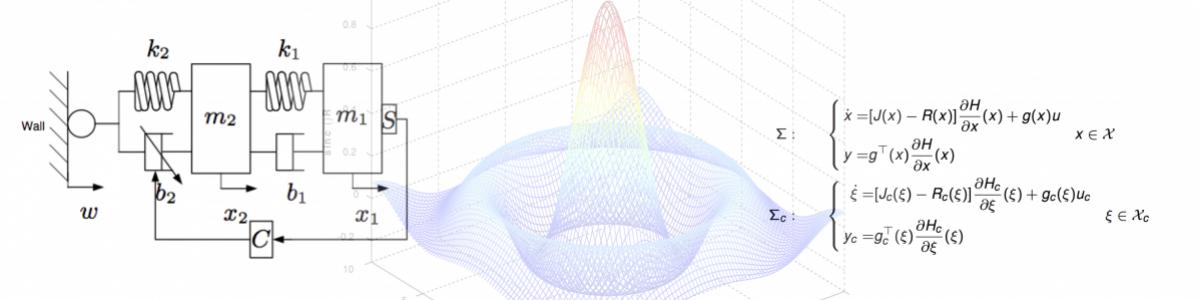
Conservation of energy is a fundamental property shared by all physical systems. This feature is the base of physical modeling through the formalization of generalized interconnection laws (Kirchhof's law). Bond-graphs, linear graphs and other network models rely on this principle. In network models the system is considered as the interconnection of energy storing elements together with energy dissipating elements via basic physical interconnection laws. The port-Hamiltonian framework formalizes this interconnection by a power preserving geometric structure, and defines the Hamiltonian function as the total energy stored in a system, thus, port-Hamiltonian systems (PHS) have direct physical interpretation and particular geometric structure. Models based on energy approaches are very useful tools for engineers, since they are defined in terms of energy, which is a concept common to all engineering domains. They are specially interesting for control design since the closed loop energy function is a good Lyapunov candidate function for non linear control. It is particularly suited for passivity based control methods.
At the end of the course it is expected that the students will master the following topics:
-
Formulation of simple lumped and distributed parameter dynamical systems using PHS models.
-
Structured modeling of complex and multi-physical systems by interconnection of simple PHS and irreversible PHS models.
-
Passivity based control of nonlinear system and simple distributed parameter sytems using the PHS formulation.
Content
In this course the basic concepts of energy based modeling and their use for the modeling and control of simple and complex physical systems will be revised.
-
In a irst part we study models arising from physical balance equations. The port-Hamiltonian model is derived for classes of (linear and non-linear) mechanical, electrical and electro-mechanical systems and it is shown how models of complex physical systems can be constructed systematically via the interconnection of simple sub-systems. We show how the approach is naturally extended to the modeling of multi-physical systems, i.e., systems arising from the interconnection of different physical domains In this part we also introduce the concepts of Irreversible port Hamiltonian systems and infinite dimensional port Hamiltonian systems in oder to cope with oupled mechanic-thermodynamic systems and distributed parameter systems respectively.
-
In a second part we show how the PHS structure can be use for control design. This is particularly useful for the control of systems described by non-linear or/and distributed parameter models. For this purpose we revise the theory of passivity based control and specialize it to PHS. It is shown how the energy function and the PHS structure is instrumental to derive Lyapunov functions and how the approaches naturally lead to the well known Casimir method and Interconnection and Damping Assignment – Passvity Based Control (IDA-PBC).
-
The third part is devoted to irreversible and distributed parameter systems. In these two cases we show how the original port Hamiltonian formalism can be adapted to cope with these two particular properties. In particular, the control synthesis detailed in the second part of this course will be extended to cope with open thermodynamic systems described by irreversible PHS and distributed parameter systems described by infinite dimensional PHS.
Each part will be divided into two lectures of 2 hours each. One 3 hours session of practical work using Matlab will be used to develop a small project/case study. The titles of each lecture/exercise session are
-
Modeling of physical systems systems: from black box to structured modeling
-
Balance equations, conservation laws, and passive systems: the Port-Hamiltonian framework.
-
Passivity, stability and performances.
-
Passivity Based Control (PBC) design for linear and non linear PHS.
-
Irreversible PHS : modelling and control
-
Infinite dimensional PHS: modelling and control
-
Case study session: Control synthesis using IDA-PBC.
The support material will be mainly based on the following textbooks:
[1] Duindam, V.; Macchelli, A.; Stramigioli, S.; Bruyninckx, H (2009). Modeling And Control Of Complex Physical Systems. Springer Verlag.
[2] A.J. Van der Schaft and D. Jeltsema (2014), “Port-Hamiltonian Systems Theory: An Introductory Overview“, Foundations and Trends in Systems and Control, NOW Publishing Inc., 188 pages, 2014. (ISBN: 978-1-60198-786-0).
[3] B. Jacob and H.J. Zwart (2012) Linear Port Hamiltonian Systems on Infinite-dimensional Spaces, Birkhäuser Basel.
Material
Stability, passivity, control of PHS
Irreversible Port Hamiltonian Systems
Infinite dimensional Port Hamiltonian Systems
Infinite dimensional Port Hamiltonian Systems
Infinite dimensional Port Hamiltonian Systems
2015 Project